Radio theory and link planning for Wireless LAN (WLAN)
Version française
En español (by Active Matrix in Argentina)
Versione italiana (by Diego in Italy)
Power
Power is expressed in Watts or in the Decibel relative units compared to milliwatts (dBm).
Conversion from Watts (W) to decibels "milliwatts" (dBm) :
(dBm= 10*log10(P/ 0.001))
Loss in a coaxial cable at 2.45 GHz
Here are some loss value for common coaxial cables:
Antenna
Parabolic antenna:
Here's the maximum theoretical gain of a parabolic antenna:
Radiated power
Radiated power (power sent by the antenna) can be easily computed (in dBm):
Radiated power [dBm] = Transmitter power [dBm] - cable loss [dB] + antenna gain[dBi]
Free space loss
It is the power loss of wave travelling in free space (whithout obstacles).
Correspondance between free space gain loss in dB and distance in kilometer (km) :
(Friis formula)
Receiver sensitivity
Receiver has a minimum received power threshold (on the card connector) that the signal must have to achieve a certain bitrate. If the signal power is lower the maximum achievable bitrate will be decreased or performance will decrease. So we have better use receiver with low threshold value, here are some typical receiver sensitivity values:
(These are values given by the manufacturer).
Signal to Noise Ratio
Receiver sensitivity is not the only parameter for the receiver, we have also to take into account the signal to noise power ratio. It's the minimum power difference to achieve between the wanted received signal and the noise (thermal noise, industrial noise due for example to microwave ovens, interering noise due to other WLAN on the same frequency band). It is defined as:
Signal/Noise Ratio [dB] = 10 * Log10 (Signal Power [W] / Noise Power [W])
If the signal is more powerful than the noise, signal/noise ratio (also called S/N ratio) will be positive. If the signal is buried in the noise, the ratio will be negative. In order to be able to work at a certain data rate the system needs a minimum S/N ratio:
If the noise level is very low then the system will be limited more by the receiver sensitivity than by the S/N ratio. If the noise level is high then it will be the Signal/Noise ratio that will count to achieve a given data rate. If the noise level is high we will need more received power. In normal conditions whithout any other WLAN on the frequency and whithout industrial noise the noise level will be around -100dBm. For example to achieve a 11 Mbps data rate with an Orinoco 802.11b card we would need a received power 16dB higher (S/N ratio) so a level of -100+16=-84 dBm but in fact the minimum receiver sensitivity is at -82 dBm...higher than -84. It means in that case the mimimum receiver sensitivity is the limiting factor for the system.
Link budget
Link budget is the computation of the whole transmission chain. Here's a budget for free space loss transmission:
Link working condition is that the total : Total Transmit + Total Propagation + Total Receive must be greater than 0 . The remain gives the margin of the system.
Warning: These rules are theoretical. It represents the maximum achievable for a system. In reality we will have interferences (other WLAN networks, bluetooth), industrial noise (microwave ovens), atmospheric losses (air moisture, scattering, refraction), badly pointed antenna, reflexions,... that will affect performances. It is so necessary to take a sufficient security margin (5-6 dB or more on large distances).
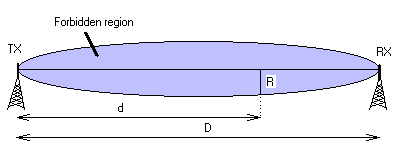
Propagation: Fresnel ellipsoid

A simple and quick explanation of Fresnel ellispsoid role in radio propagation is to see the thing like a virtual "pipe" where most of the energy travels between a transmitting and receiving site. So in order to avoid losses there should be NO obstacles inside this zone (forbidden region) because an obstacle will disturb "the energy flow". (the explanation is really simplified !).
For example, if half of the forbidden zone is masked (antenna at the limit of line of sight), there will be a signal power loss of 6 dB (power loss of 75 %).
(The radius of forbidden region here is 0.6 x Radius of first Fresnel ellipsoid)
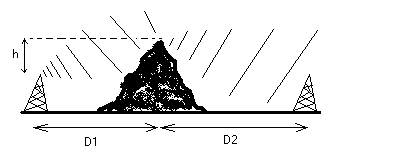
Propagation: Diffraction
When an obstacle is located between the transmitter and the receiver some energy still pass through thanks to the diffraction phenomenon on the top edge of the obstacle. The higher the frequency of the transmission the higher the loss will be.
Propagation: Polarisation
Wave polarisation is given by the type of your antenna and its orientation (radiating element) respectively to the ground . For a example a whip antenna will give a vertical polarised wave when set vertically ( | ) and horizontal polarisation when lying horizontal (--). The same hold for Yagi antennas ( |-|-|-| ). Helical antennas produce neither vertical nor horizontal polarisation but circular polarisation. Circular polarisation can turn either right or left...like normal cork openers and joke cork openers ;-)
Practically in a transmission system transmitter and receiver antennas should have the same polarisation for best performance. (As polarisation change with diffractions and reflection this rule does not always hold). Vertical polarisation is prefered for long range transmission because the ground effect attenuate the signal power in horizontal polarisation case in long range.
A transmission system with circular polarisation antennas is a good way to attenuate the effect of reflections (principle used for GPS).
Reflections and delay spread
Radio waves reflect ont the obstacles they meet. At the receiver side we catch then at the same time the direct wave (if in line of sight) and the reflected waves. This leads to canceled power at certain frequencies and also a time difference between the different received components that makes the received signal spread in the time domain. Consequence on the system is harmful and lead to decreased performances (transmission errors). In order to reduce this effect the receiver has what we call an equaliser that counteract these faults. Anyway this has a limited capacity and manufacturers give delay spread limit in order to achieve minimum error rate at a certain data rate:
We see that for higher bit rate we have better not having to long reflections. The time difference for a reflection can be easily calculated as radio wave travel at the speed of light (300'000'000 m/s):
Time difference [s] = Length difference between direct path and reflected path [m] / 300'000'000
So a time difference of 50 nanoseconds corresponds to a path length difference of 15 meters. In order to minimise the reflection rate it is better using directive antennas, be in line of sight. Another possibility is also to use circular wave polarisation antennas (helical antenna) that cancel quite well the first reflexions.
Reflections also exists in the ensemble coaxial cable-connectors-antennas if these are not well adapted and designed (bad impedance, badly tuned antenna => standing waves, bad SWR) and so may lead to transmission errors.
Warning ! The delay spread value correspond to a
computation that involve the level and time difference of every
component:
Delay spread [s] = sum on all components of { (component weight)
* (component time difference) }
References, documentation
© Mathias Coinchon - Last updated 13.1.2003 v2.0 - Home